Patrícia - Atividade 2 - "Quem sou eu?" - Quadriláteros

Nome da atividade: “Quem sou eu?” - Quadriláteros

Ano de escolaridade: 3.º / 4.º

Materiais: - Conjunto de quadriláteros;

                  - Verificador de ângulos retos (círculo dobrado em 4);

                  - Lápis;

                  - Quadro de giz;

                  - Quadro interativo.

Conteúdos: Geometria e Medida – Figuras Geométricas

- Comparação das amplitudes de ângulos;

- Ângulos retos, agudos e obtusos;

- Retângulos como quadriláteros de ângulos retos;

- Polígonos regulares.

Metas: Geometria e Medida - Figuras geométricas

- Identificar e comparar ângulos;

- Reconhecer propriedades geométricas.

Descrição e reflexão:

Esta atividade começa com a pergunta “O que são quadriláteros?”, ao que muitos alunos responderam “figura com quatro lados”, então desenho uma coisa deste género                  

E questiono se este seria, mas a resposta foi quase automática “tem de estar ligado”, então desenho 

Esta imagem gera alguma controvérsia, uns dizem que sim, outros dizem que não, justificando que os lados “não podem cruzar-se”. Após alguma discussão chegamos à conclusão de que são dois triângulos e que o desenho não pode ser considerado um quadrilátero.

Logo em seguida desenho

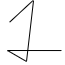
E os alunos dizem “tem de estar fechado!”. Então, finalmente, completo a imagem acima e os alunos afirmam que aquele é um quadrilátero.

O passo seguinte foi relembrar a definição de quadrilátero e nomear alguns dos quadriláteros “especiais” que conheciam e quais as suas características. Completámos o esquema no quadro interativo.

A atividade prosseguiu com a distribuição de um conjunto de quadriláteros por aluno e a explicação das regras do jogo, em que um aluno escolheria um quadrilátero e os outros colocariam questões para descobrir qual era o escolhido, sem nunca dizerem o nome dele, obtendo apenas a resposta SIM ou NÃO.

Alguns alunos ficaram sem saber o que haveriam de questionar, mas após ser feito o paralelismo com o jogo “Quem é quem?”, houve logo exemplos de perguntas. A turma chegou à conclusão de que a amplitude dos ângulos seria uma característica pertinente, assim, antes de começar a jogar, optou por verificar quais eram ângulos retos e marcá-los.
Ao longo do jogo, os alunos aperceberam-se que existiam questões que eliminavam um maior número de peças do que outras e que essas deveriam ser feitas em primeiro lugar.
Esta atividade poderia evoluir para o trabalho com diagramas de Venn, reforçando as características distintivas dos vários tipos de quadriláteros.

Numa próxima aplicação desta atividade talvez opte por fazer o jogo primeiro, de modo a perceber o que ainda recordam e só depois fazer a sistematização das características dos quadriláteros, com o preenchimento do esquema.
Este jogo poderá também ser aplicado aos sólidos geométricos, para revisão dos mesmos e dos conceitos que lhes estão associados.